Los Polinomios:
*Polinomios de una variable
Para a0, …, an constantes en algún anillo (en particular podemos tomar un cuerpo, como  o
o  , en cuyo caso los coeficientes del polinomio serán números) con an distinto de cero y
, en cuyo caso los coeficientes del polinomio serán números) con an distinto de cero y  , entonces un polinomio,
, entonces un polinomio,  , de grado n en la variable x es un objeto de la forma
, de grado n en la variable x es un objeto de la forma
 o
o  , en cuyo caso los coeficientes del polinomio serán números) con an distinto de cero y
, en cuyo caso los coeficientes del polinomio serán números) con an distinto de cero y  , entonces un polinomio,
, entonces un polinomio,  , de grado n en la variable x es un objeto de la forma
, de grado n en la variable x es un objeto de la forma
El polinomio se puede escribir más concisamente usando sumatorios como
Las constantes a0, …, an se llaman los coeficientes del polinomio. A a0 se le llama el coeficiente constante (o término independiente) y a an, el coeficiente principal. Cuando el coeficiente principal es 1, al polinomio se le llama mónico o normado.
*Polinomios de varias variable
Los polinomios de varias variables, a diferencia de los de una variable, tienen en total más de una variable. Por ejemplo los monomios:
En detalle el último de ellos  es un momonio de tres variables (ya que en él aparecen las tres letras x, y y z), el coeficiente es 4, y los exponentes son 1, 2 y 1 de x, y y z respectivamente.
es un momonio de tres variables (ya que en él aparecen las tres letras x, y y z), el coeficiente es 4, y los exponentes son 1, 2 y 1 de x, y y z respectivamente.
 es un momonio de tres variables (ya que en él aparecen las tres letras x, y y z), el coeficiente es 4, y los exponentes son 1, 2 y 1 de x, y y z respectivamente.
es un momonio de tres variables (ya que en él aparecen las tres letras x, y y z), el coeficiente es 4, y los exponentes son 1, 2 y 1 de x, y y z respectivamente.
Operaciones con Polinomios:
Los polinomios se pueden sumar y restar agrupando los términos y simplificando los monomios semejantes. Para multiplicar polinomios se multiplica cada término de un polinomio por cada uno de los términos del otro polinomio y luego se simplifican los monomios semejantes.
- Ejemplo
Sean los polinomios: 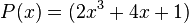 y
y 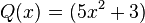 , entonces el producto es:
, entonces el producto es:
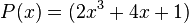 y
y 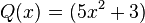 , entonces el producto es:
, entonces el producto es:
Para poder realizar eficazmente la operación se tiene que adquirir los datos necesarios de mayor a menor. Una fórmula analítica que expresa el producto de dos polinomios es la siguiente:
Aplicando esta fórmula al ejemplo anterior se tiene:
Puede comprobarse que para polinomios no nulos se satisface la siguiente relación entre el grado de los polinomios  y
y  y el polinomio producto
y el polinomio producto  :
:
 y
y  y el polinomio producto
y el polinomio producto  :
:(*)
Puesto que el producto de cualquier polinomio por el polinomio nulo es el propio polinomio nulo, se define convencionalmente que  (junto con la operación
(junto con la operación  ) por lo que la expresión () puede extenderse también al caso de que alguno de los polinomios sea nulos.
) por lo que la expresión () puede extenderse también al caso de que alguno de los polinomios sea nulos.
 (junto con la operación
(junto con la operación  ) por lo que la expresión () puede extenderse también al caso de que alguno de los polinomios sea nulos.
) por lo que la expresión () puede extenderse también al caso de que alguno de los polinomios sea nulos.
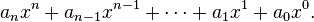
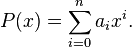
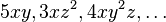






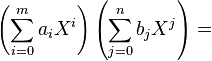



No hay comentarios:
Publicar un comentario